
들어가며
오늘은 특정한 몇몇 요소끼리의 순서가 정해진 상황에서 사용할 수 있는 정렬 방법인 위상 정렬(Topological sorting)에 대하여 알아보겠습니다.
알고리즘
수학에서 위상(topology)이란 연속적인 힘에 의한 변형에도 유지되는 기하학적인 속성을 의미합니다. 이렇게만 말하면 와닿지 않으니 갓 나온 가래떡을 하나 떠올려봅시다. 길쭉한 원기둥 모양을 한 가래떡에 찢어지지 않을 정도로 적당한 힘을 가하면 원래 모양보다 늘어나거나 구부러집니다.

그러나 가래떡의 모양이 변했다고 해서 원래 가지고 있던 속성들이 모두 변하는 것은 아닙니다. 아래 그림을 한 번 보겠습니다.


예를 들어, 이렇게 가래떡을 구성하는 분자들끼리 연결된 상태들은 변하지 않죠. 여전히 서로를 꽉 붙잡고 있습니다.
이렇게 서로간의 연결성이나 근접성, 분리 여부 등 단순한 변형에도 변하지 않는 요소 간의 관계에 대한 속성과 구조, 성질등을 다루는 학문을 위상 수학이라고 부릅니다. 제대로 설명하면 훨씬 더 복잡하고 깊지만, 우리는 위상 정렬에 대해서만 공부하는 것이니 이 정도의 감만 잡고 넘어가겠습니다.
위상 정렬도 위의 개념과 마찬가지로, 그래프 상의 정점들이 갖는 특정한 순서를 만족시키도록 하는 선행 관계를 활용하여 요소들을 나열하는 정렬 알고리즘을 말합니다. 이를 어떻게 하면 코드로 구현할 수 있을지, 정렬 과정을 생각해보겠습니다.
예시로 다섯개의 정점 1, 2, 3, 4, 5 가 있고, 이 요소들을 나열할때 아래 몇 가지 순서가 지켜져야 한다는 상황을 가정하겠습니다.
- 1은 2보다 앞에 있어야 한다.
- 3은 5보다 앞에 있어야 한다.
- 2는 4보다 앞에 있어야 한다.

위상 정렬의 핵심 키워드는 진입 차수입니다. 진입 차수란 정점이 얼마만큼의 선행 조건을 가지고 있는지를 나타내는 수입니다. 즉, 1은 2 앞에 있어야 하고, 2는 4 앞에 있어야 하므로 2와 4의 진입 차수는 1이 됩니다. 반대로 1과 3의 경우 별다른 선행 조건이 없기 때문에 진입 차수는 0이 됩니다.
먼저 진입 차수가 0인 정점들을 방문하고, 방문한 정점이 다른 정점의 선행 조건으로 연결된 정점의 진입 차수를 하나씩 빼주면서 정렬을 수행합니다.
이런식으로 모든 정점을 방문하게 되면 정렬이 끝나고 우리가 원하는 조건을 만족하는 순서를 찾을 수 있게 됩니다. 아래부터는 알고리즘의 시나리오에 따라 한 단계씩 수행하는 모습입니다.
- 진입 차수가 0인 정점을 큐에 추가한다. (1, 3)

진입 차수가 0인 정점을 큐에 추가해줍니다. 조건에 만족하는 1, 3 정점을 큐에 추가하였습니다.
- 큐의 가장 앞쪽 정점을 방문한다. (1)

큐의 가장 앞쪽에 있던 정점인 1을 방문합니다. 방문과 동시에 결과 배열인 result로 옮기고, 1을 선행 조건으로 갖는 정점들의 진입 차수를 1만큼 낮춥니다. 따라서 2의 진입 차수가 1에서 0이 되었습니다.
- 큐의 가장 앞쪽 정점을 방문한다. (3)

이 작업은 큐가 빌때까지 반복합니다. 마찬가지로 큐의 가장 앞쪽에 있던 정점인 3을 방문합니다. 3을 result 배열로 옮기고, 3을 선행 조건으로 갖던 5의 진입 차수를 낮춰줍니다.
- 큐가 비면, 진입 차수가 0인 정점을 큐에 추가한다. (2, 5)
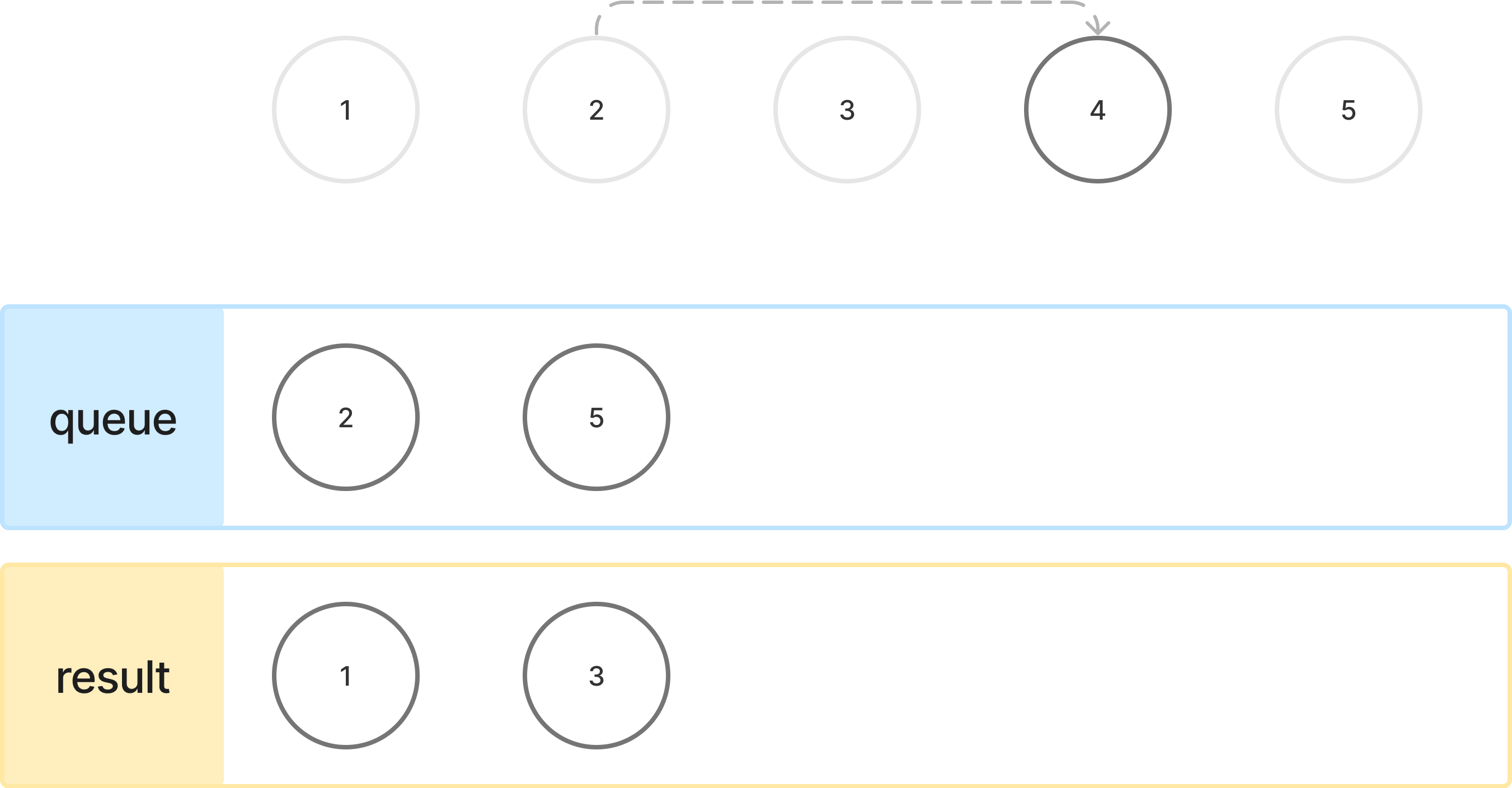
큐가 비었으므로, 다시 진입 차수가 0인 정점들을 큐에 추가해주었습니다. 정점 2와 5가 새로 큐에 들어오게 되었습니다.
- 큐의 가장 앞쪽 정점을 방문한다. (2)

마찬가지로 큐의 앞쪽 정점부터 방문해줍니다. 선행 조건으로 갖던 4의 진입 차수가 0이 되었고, 정점 2는 result 배열에 추가됩니다.
- 큐의 가장 앞쪽 정점을 방문한다. (5)

큐에 남은 정점인 5도 방문해줍니다. 5를 선행 조건으로 갖는 정점은 없기 때문에 따로 진입 차수를 수정하지는 않았습니다.
- 진입 차수가 0인 정점을 큐에 추가한다. (4)

남은 정점 4를 큐에 추가하고, 그대로 방문하면 정렬이 마무리됩니다.
- 정렬 완료

이런 방식을 통해 선행 조건을 만족하는 순서를 찾을 수 있었습니다.
아래는 자바스크립트로 구현한 위상 정렬 코드입니다.
구현
const node = [1, 2, 3, 4, 5]; // 정점
const edge = [[2], [4], [5], [], []]; // 선행 조건
const degree = [0, 0, 0, 0, 0]; // 진입 차수
const queue = []; // 큐
const result = []; // 결과 배열
edge.forEach((destinationArray) => {
destinationArray.forEach((destinationNode) => {
degree[destinationNode-1]++;
});
});
for (let i = 0; i < node.length; i++) {
if (degree[i] === 0) {
queue.push(i);
}
}
for (let i = 0; i < node.length; i++) {
const currentNode = queue.shift();
result.push(currentNode+1);
for (let destinationNode of edge[currentNode]) {
degree[destinationNode-1]--;
if (degree[destinationNode-1] === 0) {
queue.push(destinationNode-1);
}
}
}
console.log(result);
마치며
오늘은 위상 정렬에 대해서 알아보았습니다. 위상 정렬은 순환이 생기는 모순된 구조에서는 사용할 수 없습니다. 이러한 성질을 이용하여 역으로 그래프에서 순환이 생기는 부분을 확인할 수 있기도 합니다. 위상 정렬을 적용하기 전 그래프의 상태를 잘 확인하고 사용하는 것이 좋겠습니다.
긴 글 읽어주셔서 감사합니다.
'이론 > 알고리즘' 카테고리의 다른 글
| 최단 경로 찾기 : 플로이드 워셜(Floyd-Warshall) 알고리즘 (0) | 2023.05.21 |
|---|---|
| 최단 경로 찾기 : 다익스트라(Dijkstra) 알고리즘 (0) | 2023.04.02 |
| 그래프 탐색하기 : BFS와 DFS (0) | 2023.03.24 |
| [C++] 백준 13549번: 숨바꼭질 3 (0) | 2021.10.07 |
| [C++] BOJ 에서 정해지지 않은만큼의 입력을 받을 때 (0) | 2021.08.24 |




댓글